Metric space
In mathematics, a metric space is a set where a notion of distance (called a metric) between elements of the set is defined.
The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space. In fact, the notion of "metric" is a generalization of the Euclidean metric arising from the four long-known properties of the Euclidean distance. The Euclidean metric defines the distance between two points as the length of the straight line segment connecting them.
The geometric properties of the space depend on the metric chosen, and by using a different metric we can construct interesting non-Euclidean geometries such as those used in the theory of general relativity.
A metric space also induces topological properties like open and closed sets which leads to the study of even more abstract topological spaces.
History
Maurice Fréchet introduced metric spaces in his work Sur quelques points du calcul fonctionnel, Rendic. Circ. Mat. Palermo 22 (1906) 1–74.
Definition
A metric space is an ordered pair 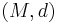 where
where  is a set and
is a set and  is a metric on
is a metric on  , i.e., a function
, i.e., a function
such that for any 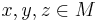 , the following holds:
, the following holds:
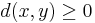 (non-negative) ,
(non-negative) ,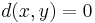 iff
iff 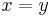 (identity of indiscernibles),
(identity of indiscernibles), (symmetry) and
(symmetry) and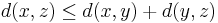 (triangle inequality) .
(triangle inequality) .
The first condition follows from the other three, since:
The function  is also called distance function or simply distance. Often,
is also called distance function or simply distance. Often,  is omitted and one just writes
is omitted and one just writes  for a metric space if it is clear from the context what metric is used.
for a metric space if it is clear from the context what metric is used.
Examples of metric spaces
- Ignoring mathematical details, for any system of roads and terrains the distance between two locations can be defined as the length of the shortest route connecting those locations. To be a metric there shouldn't be any one-way roads. The triangle inequality expresses the fact that detours aren't shortcuts. Many of the examples below can be seen as concrete versions of this general idea.
- The real numbers with the distance function
 given by the absolute difference, and more generally Euclidean
given by the absolute difference, and more generally Euclidean  -space with the Euclidean distance, are complete metric spaces. The rational numbers with the same distance also form a metric space, but are not complete.
-space with the Euclidean distance, are complete metric spaces. The rational numbers with the same distance also form a metric space, but are not complete. - The positive real numbers with distance function
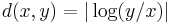 is a complete metric space.
is a complete metric space. - Any normed vector space is a metric space by defining
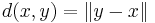 , see also relation of norms and metrics. (If such a space is complete, we call it a Banach space.) Examples:
, see also relation of norms and metrics. (If such a space is complete, we call it a Banach space.) Examples:
- The Manhattan norm gives rise to the Manhattan distance, where the distance between any two points, or vectors, is the sum of the differences between corresponding coordinates.
- The maximum norm gives rise to the Chebyshev distance or chessboard distance, the minimal number of moves a chess king would take to travel from
 to
to  .
.
- The British Rail metric (also called the Post Office metric or the SNCF metric) on a normed vector space is given by
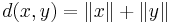 for distinct points
for distinct points  and
and  , and
, and 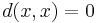 . More generally
. More generally  can be replaced with a function
can be replaced with a function  taking an arbitrary set
taking an arbitrary set  to non-negative reals and taking the value
to non-negative reals and taking the value  at most once: then the metric is defined on
at most once: then the metric is defined on  by
by 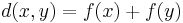 for distinct points
for distinct points  and
and  , and
, and 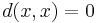 . The name alludes to the tendency of railway journeys (or letters) to proceed via London (or Paris) irrespective of their final destination.
. The name alludes to the tendency of railway journeys (or letters) to proceed via London (or Paris) irrespective of their final destination. - If
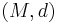 is a metric space and
is a metric space and  is a subset of
is a subset of  , then
, then 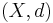 becomes a metric space by restricting the domain of
becomes a metric space by restricting the domain of  to
to 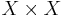 .
. - The discrete metric, where
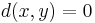 if
if 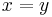 and
and 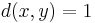 otherwise, is a simple but important example, and can be applied to all non-empty sets. This, in particular, shows that for any non-empty set, there is always a metric space associated to it. Using this metric, any point is an open ball, and therefore every subset is open and the space has the discrete topology.
otherwise, is a simple but important example, and can be applied to all non-empty sets. This, in particular, shows that for any non-empty set, there is always a metric space associated to it. Using this metric, any point is an open ball, and therefore every subset is open and the space has the discrete topology. - A finite metric space is a metric space having a finite number of points. Not every finite metric space can be isometrically embedded in a Euclidean space.[1][2]
- The hyperbolic plane is a metric space. More generally:
- If
 is any connected Riemannian manifold, then we can turn
is any connected Riemannian manifold, then we can turn  into a metric space by defining the distance of two points as the infimum of the lengths of the paths (continuously differentiable curves) connecting them.
into a metric space by defining the distance of two points as the infimum of the lengths of the paths (continuously differentiable curves) connecting them. - If
 is some set and
is some set and  is a metric space, then, the set of all bounded functions
is a metric space, then, the set of all bounded functions 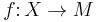 (i.e. those functions whose image is a bounded subset of
(i.e. those functions whose image is a bounded subset of  ) can be turned into a metric space by defining
) can be turned into a metric space by defining 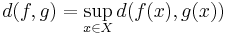 for any two bounded functions
for any two bounded functions  and
and  (where
(where 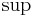 is supremum.[3] This metric is called the uniform metric or supremum metric, and If
is supremum.[3] This metric is called the uniform metric or supremum metric, and If  is complete, then this function space is complete as well. If X is also a topological space, then set of all bounded continuous functions from
is complete, then this function space is complete as well. If X is also a topological space, then set of all bounded continuous functions from  to
to  (endowed with the uniform metric), will also be a complete metric if M is.
(endowed with the uniform metric), will also be a complete metric if M is. - If
 is an undirected connected graph, then the set
is an undirected connected graph, then the set  of vertices of
of vertices of  can be turned into a metric space by defining
can be turned into a metric space by defining 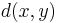 to be the length of the shortest path connecting the vertices
to be the length of the shortest path connecting the vertices  and
and  . In geometric group theory this is applied to the Cayley graph of a group, yielding the word metric.
. In geometric group theory this is applied to the Cayley graph of a group, yielding the word metric. - The Levenshtein distance is a measure of the dissimilarity between two strings
 and
and  , defined as the minimal number of character deletions, insertions, or substitutions required to transform
, defined as the minimal number of character deletions, insertions, or substitutions required to transform  into
into  . This can be thought of as a special case of the shortest path metric in a graph and is one example of an edit distance.
. This can be thought of as a special case of the shortest path metric in a graph and is one example of an edit distance. - Given a metric space
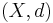 and an increasing concave function
and an increasing concave function 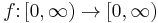 such that
such that 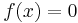 if and only if
if and only if 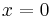 , then
, then 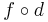 is also a metric on
is also a metric on  .
. - Given an injective function
 from any set
from any set  to a metric space
to a metric space 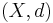 ,
, 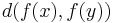 defines a metric on
defines a metric on  .
. - Using T-theory, the tight span of a metric space is also a metric space. The tight span is useful in several types of analysis.
- The set of all
 by
by  matrices over some field is a metric space with respect to the rank distance
matrices over some field is a metric space with respect to the rank distance 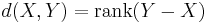 .
. - The Helly metric is used in game theory.
Open and closed sets, topology and convergence
Every metric space is a topological space in a natural manner, and therefore all definitions and theorems about general topological spaces also apply to all metric spaces.
About any point  in a metric space
in a metric space  we define the open ball of radius
we define the open ball of radius 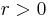 about
about  as the set
as the set
These open balls generate a topology on M, making it a topological space.
Explicitly, a subset  of
of  is called open if for every
is called open if for every  in
in  there exists an
there exists an 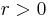 such that
such that 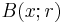 is contained in
is contained in  . The complement of an open set is called closed. A neighborhood of the point
. The complement of an open set is called closed. A neighborhood of the point  is any subset of
is any subset of  that contains an open ball about
that contains an open ball about  as a subset.
as a subset.
A topological space which can arise in this way from a metric space is called a metrizable space; see the article on metrization theorems for further details.
A sequence (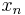 ) in a metric space
) in a metric space  is said to converge to the limit
is said to converge to the limit 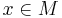 iff for every
iff for every 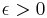 , there exists a natural number N such that
, there exists a natural number N such that 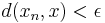 for all
for all  . Equivalently, one can use the general definition of convergence available in all topological spaces.
. Equivalently, one can use the general definition of convergence available in all topological spaces.
A subset  of the metric space
of the metric space  is closed iff every sequence in
is closed iff every sequence in  that converges to a limit in
that converges to a limit in  has its limit in
has its limit in  .
.
Types of metric spaces
Complete spaces
A metric space  is said to be complete if every Cauchy sequence converges in
is said to be complete if every Cauchy sequence converges in  . That is to say: if
. That is to say: if 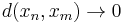 as both
as both  and
and  independently go to infinity, then there is some
independently go to infinity, then there is some 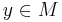 with
with 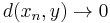 .
.
Every Euclidean space is complete, as is every closed subset of a complete space. The rational numbers, using the absolute value metric  , are not complete.
, are not complete.
Every metric space has a unique (up to isometry) completion, which is a complete space that contains the given space as a dense subset. For example, the real numbers are the completion of the rationals.
If  is a complete subset of the metric space
is a complete subset of the metric space  , then
, then  is closed in
is closed in  . Indeed, a space is complete iff it is closed in any containing metric space.
. Indeed, a space is complete iff it is closed in any containing metric space.
Every complete metric space is a Baire space.
Bounded and totally bounded spaces
A metric space M is called bounded if there exists some number r, such that d(x,y) ≤ r for all x and y in M. The smallest possible such r is called the diameter of M. The space M is called precompact or totally bounded if for every r > 0 there exist finitely many open balls of radius r whose union covers M. Since the set of the centres of these balls is finite, it has finite diameter, from which it follows (using the triangle inequality) that every totally bounded space is bounded. The converse does not hold, since any infinite set can be given the discrete metric (one of the examples above) under which it is bounded and yet not totally bounded.
Note that in the context of intervals in the space of real numbers and occasionally regions in a Euclidean space Rn a bounded set is referred to as "a finite interval" or "finite region". However boundedness should not in general be confused with "finite", which refers to the number of elements, not to how far the set extends; finiteness implies boundedness, but not conversely.
Compact spaces
A metric space M is compact if every sequence in M has a subsequence that converges to a point in M. This is known as sequential compactness and, in metric spaces (but not in general topological spaces), is equivalent to the topological notions of countable compactness and compactness defined via open covers.
Examples of compact metric spaces include the closed interval [0,1] with the absolute value metric, all metric spaces with finitely many points, and the Cantor set. Every closed subset of a compact space is itself compact.
A metric space is compact iff it is complete and totally bounded. This is known as the Heine–Borel theorem. Note that compactness depends only on the topology, while boundedness depends on the metric.
Lebesgue's number lemma states that for every open cover of a compact metric space M, there exists a "Lebesgue number" δ such that every subset of M of diameter < δ is contained in some member of the cover.
Every compact metric space is second countable,[4] and is a continuous image of the Cantor set. (The latter result is due to Pavel Alexandrov and Urysohn.)
Locally compact and proper spaces
A metric space is said to be locally compact if every point has a compact neighborhood. Euclidean spaces are locally compact, but infinite-dimensional Banach spaces are not.
A space is proper if every closed ball {y : d(x,y) ≤ r} is compact. Proper spaces are locally compact, but the converse is not true in general.
Connectedness
A metric space  is connected if the only subsets that are both open and closed are the empty set and
is connected if the only subsets that are both open and closed are the empty set and  itself.
itself.
A metric space  is path connected if for any two points
is path connected if for any two points 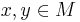 there exists a continuous map
there exists a continuous map ![f\colon [0,1] \to M](/2012-wikipedia_en_all_nopic_01_2012/I/3f77e15197776b9b950b6023f3cdc6ea.png) with
with 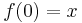 and
and 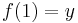 . Every path connected space is connected, but the converse is not true in general.
. Every path connected space is connected, but the converse is not true in general.
There are also local versions of these definitions: locally connected spaces and locally path connected spaces.
Simply connected spaces are those that, in a certain sense, do not have "holes".
Separable spaces
A metric space is separable space if it has a countable dense subset. Typical examples are the real numbers or any Euclidean space. For metric spaces (but not for general topological spaces) separability is equivalent to second countability and also to the Lindelöf property.
Types of maps between metric spaces
Suppose (M1,d1) and (M2,d2) are two metric spaces.
Continuous maps
The map f:M1→M2 is continuous if it has one (and therefore all) of the following equivalent properties:
- General topological continuity
- for every open set U in M2, the preimage f -1(U) is open in M1
- This is the general definition of continuity in topology.
- Sequential continuity
- if (xn) is a sequence in M1 that converges to x in M1, then the sequence (f(xn)) converges to f(x) in M2.
- This is sequential continuity, due to Eduard Heine.
- ε-δ definition
- for every x in M1 and every ε>0 there exists δ>0 such that for all y in M1 we have
- This uses the (ε, δ)-definition of limit, and is due to Augustin Louis Cauchy.
Moreover, f is continuous if and only if it is continuous on every compact subset of M1.
The image of every compact set under a continuous function is compact, and the image of every connected set under a continuous function is connected.
Uniformly continuous maps
The map ƒ : M1 → M2 is uniformly continuous if for every ε > 0 there exists δ > 0 such that
Every uniformly continuous map ƒ : M1 → M2 is continuous. The converse is true if M1 is compact (Heine–Cantor theorem).
Uniformly continuous maps turn Cauchy sequences in M1 into Cauchy sequences in M2. For continuous maps this is generally wrong; for example, a continuous map from the open interval (0,1) onto the real line turns some Cauchy sequences into unbounded sequences.
Lipschitz-continuous maps and contractions
Given a number K > 0, the map ƒ : M1 → M2 is K-Lipschitz continuous if
Every Lipschitz-continuous map is uniformly continuous, but the converse is not true in general.
If K < 1, then ƒ is called a contraction. Suppose M2 = M1 and M1 is complete. If ƒ is a contraction, then ƒ admits a unique fixed point (Banach fixed point theorem). If M1 is compact, the condition can be weakened a bit: ƒ admits a unique fixed point if
for all 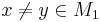 .
.
Isometries
The map f:M1→M2 is an isometry if
Isometries are always injective; the image of a compact or complete set under an isometry is compact or complete, respectively. However, if the isometry is not surjective, then the image of a closed (or open) set need not be closed (or open).
Quasi-isometries
The map f : M1 → M2 is a quasi-isometry if there exist constants A ≥ 1 and B ≥ 0 such that
and a constant C ≥ 0 such that every point in M2 has a distance at most C from some point in the image f(M1).
Note that a quasi-isometry is not required to be continuous. Quasi-isometries compare the "large-scale structure" of metric spaces; they find use in geometric group theory in relation to the word metric.
Notions of metric space equivalence
Given two metric spaces (M1, d1) and (M2, d2):
- They are called homeomorphic (topologically isomorphic) if there exists a homeomorphism between them (i.e., a bijection continuous in both directions).
- They are called uniformic (uniformly isomorphic) if there exists a uniform isomorphism between them (i.e., a bijection uniformly continuous in both directions).
- They are called isometric if there exists a bijective isometry between them. In this case, the two metric spaces are essentially identical.
- They are called quasi-isometric if there exists a quasi-isometry between them.
Topological properties
Metric spaces are paracompact[5] Hausdorff spaces[6] and hence normal (indeed they are perfectly normal). An important consequence is that every metric space admits partitions of unity and that every continuous real-valued function defined on a closed subset of a metric space can be extended to a continuous map on the whole space (Tietze extension theorem). It is also true that every real-valued Lipschitz-continuous map defined on a subset of a metric space can be extended to a Lipschitz-continuous map on the whole space.
Metric spaces are first countable since one can use balls with rational radius as a neighborhood base.
The metric topology on a metric space M is the coarsest topology on M relative to which the metric d is a continuous map from the product of M with itself to the non-negative real numbers.
Distance between points and sets; Hausdorff distance and Gromov metric
A simple way to construct a function separating a point from a closed set (as required for a completely regular space) is to consider the distance between the point and the set. If (M,d) is a metric space, S is a subset of M and x is a point of M, we define the distance from x to S as
- d(x,S) = inf {d(x,s) : s ∈ S}
Then d(x, S) = 0 if and only if x belongs to the closure of S. Furthermore, we have the following generalization of the triangle inequality:
- d(x,S) ≤ d(x,y) + d(y,S)
which in particular shows that the map 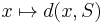 is continuous.
is continuous.
Given two subsets S and T of M, we define their Hausdorff distance to be
- dH(S,T) = max { sup {d(s,T) : s ∈ S}, sup {d(t,S) : t ∈ T} }
In general, the Hausdorff distance dH(S,T) can be infinite. Two sets are close to each other in the Hausdorff distance if every element of either set is close to some element of the other set.
The Hausdorff distance dH turns the set K(M) of all non-empty compact subsets of M into a metric space. One can show that K(M) is complete if M is complete. (A different notion of convergence of compact subsets is given by the Kuratowski convergence.)
One can then define the Gromov–Hausdorff distance between any two metric spaces by considering the minimal Hausdorff distance of isometrically embedded versions of the two spaces. Using this distance, the set of all (isometry classes of) compact metric spaces becomes a metric space in its own right.
Product metric spaces
If  are metric spaces, and N is the Euclidean norm on Rn, then
are metric spaces, and N is the Euclidean norm on Rn, then 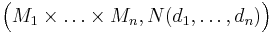 is a metric space, where the product metric is defined by
is a metric space, where the product metric is defined by
and the induced topology agrees with the product topology. By the equivalence of norms in finite dimensions, an equivalent metric is obtained if N is the taxicab norm, a p-norm, the max norm, or any other norm which is non-decreasing as the coordinates of a positive n-tuple increase (yielding the triangle inequality).
Similarly, a countable product of metric spaces can be obtained using the following metric
An uncountable product of metric spaces need not be metrizable. For example, 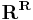 is not first-countable and thus isn't metrizable.
is not first-countable and thus isn't metrizable.
Continuity of distance
It is worth noting that in the case of a single space 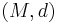 , the distance map
, the distance map 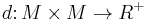 (from the definition) is uniformly continuous with respect to any of the above product metrics
(from the definition) is uniformly continuous with respect to any of the above product metrics 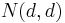 , and in particular is continuous with respect to the product topology of
, and in particular is continuous with respect to the product topology of  .
.
Quotient metric spaces
If M is a metric space with metric d, and ~ is an equivalence relation on M, then we can endow the quotient set M/~ with the following (pseudo)metric. Given two equivalence classes [x] and [y], we define
where the infimum is taken over all finite sequences 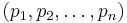 and
and 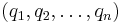 with
with ![[p_1]=[x]](/2012-wikipedia_en_all_nopic_01_2012/I/2784990f9501325a03947464b4c5e3b0.png) ,
, ![[q_n]=[y]](/2012-wikipedia_en_all_nopic_01_2012/I/87dd4683ed69ed72c19afbd0030bf949.png) ,
, ![[q_i]=[p_{i%2B1}], i=1,2,\dots, n-1](/2012-wikipedia_en_all_nopic_01_2012/I/a2929bf041992be96b5eb7ba79365e5f.png) . In general this will only define a pseudometric, i.e.
. In general this will only define a pseudometric, i.e. ![d'([x],[y])=0](/2012-wikipedia_en_all_nopic_01_2012/I/b5e33b393371174c81b951462601f03e.png) does not necessarily imply that
does not necessarily imply that ![[x]=[y]](/2012-wikipedia_en_all_nopic_01_2012/I/63be84aae0ca1995af2d779096090fdc.png) . However for nice equivalence relations (e.g., those given by gluing together polyhedra along faces), it is a metric. Moreover if M is a compact space, then the induced topology on M/~ is the quotient topology.
. However for nice equivalence relations (e.g., those given by gluing together polyhedra along faces), it is a metric. Moreover if M is a compact space, then the induced topology on M/~ is the quotient topology.
The quotient metric d is characterized by the following universal property. If 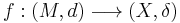 is a metric map between metric spaces (that is,
is a metric map between metric spaces (that is, 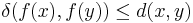 for all x, y) satisfying f(x)=f(y) whenever
for all x, y) satisfying f(x)=f(y) whenever 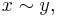 then the induced function
then the induced function 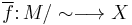 , given by
, given by ![\overline{f}([x])=f(x)](/2012-wikipedia_en_all_nopic_01_2012/I/49e9d215af2e63bffa29045e92360b20.png) , is a metric map
, is a metric map 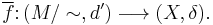
A topological space is sequential if and only if it is a quotient of a metric space.[7]
Generalizations of metric spaces
- Every metric space is a uniform space in a natural manner, and every uniform space is naturally a topological space. Uniform and topological spaces can therefore be regarded as generalizations of metric spaces.
- If we consider the first definition of a metric space given above and relax the second requirement, or remove the third or fourth, we arrive at the concepts of a pseudometric space, a quasimetric space, or a semimetric space.
- If the distance function takes values in the extended real number line R∪{+∞}, but otherwise satisfies all four conditions, then it is called an extended metric and the corresponding space is called an
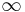 -metric space.
-metric space.
- Approach spaces are a generalization of metric spaces, based on point-to-set distances, instead of point-to-point distances.
- A continuity space is a generalization of metric spaces and posets, that can be used to unify the notions of metric spaces and domains.
Metric spaces as enriched categories
The ordered set 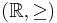 can be seen as a category by requesting exactly one morphism
can be seen as a category by requesting exactly one morphism 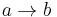 if
if 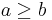 and none otherwise. By using
and none otherwise. By using 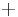 as the tensor product and
as the tensor product and  as the identity, it becomes a monoidal category
as the identity, it becomes a monoidal category 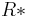 . Every metric space
. Every metric space 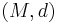 can now be viewed as a category
can now be viewed as a category 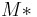 enriched over
enriched over 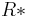 :
:
- Set
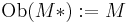
- For each
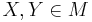 set
set 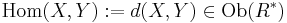
- The composition morphism
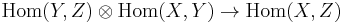 will be the unique morphism in
will be the unique morphism in 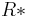 given from the triangle inequality
given from the triangle inequality 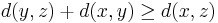
- The identity morphism
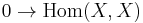 will be the unique morphism given from the fact that
will be the unique morphism given from the fact that 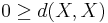 .
. - Since
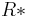 is a strict monoidal category, all diagrams that are required for an enriched category commute automatically.
is a strict monoidal category, all diagrams that are required for an enriched category commute automatically.
See the paper by F.W. Lawvere listed below.
See also
- Aleksandrov–Rassias problem
- Basic introduction to the mathematics of curved spacetime
- Category of metric spaces
- Classical Wiener space
- Glossary of Riemannian and metric geometry
- Isometry, contraction mapping and metric map
- Lipschitz continuity
- Measure (mathematics)
- Norm (mathematics)
- Premetric space
- Space (mathematics)
- Topology
- Triangle inequality
Notes
- ^ Nathan Linial. Finite Metric Spaces—Combinatorics, Geometry and Algorithms, Proceedings of the ICM, Beijing 2002, vol. 3, pp573–586
- ^ Open problems on embeddings of finite metric spaces, edited by Jirīı Matoušek, 2007
- ^ Searcóid, p. 107.
- ^ PlanetMath: a compact metric space is second countable
- ^ Rudin, Mary Ellen. A new proof that metric spaces are paracompact. Proceedings of the American Mathematical Society, Vol. 20, No. 2. (Feb., 1969), p. 603.
- ^ metric spaces are Hausdorff on PlanetMath
- ^ Goreham, Anthony. Sequential convergence in Topological Spaces. Honours' Dissertation, Queen's College, Oxford (April, 2001), p. 14
References
- Victor Bryant, Metric Spaces: Iteration and Application, Cambridge University Press, 1985, ISBN 0-521-31897-1.
- Dmitri Burago, Yu D Burago, Sergei Ivanov, A Course in Metric Geometry, American Mathematical Society, 2001, ISBN 0-8218-2129-6.
- Athanase Papadopoulos, Metric Spaces, Convexity and Nonpositive Curvature, European Mathematical Society, 2004, SBN 978-3-03719-010-4.
- Mícheál Ó Searcóid, Metric Spaces, Springer Undergraduate Mathematics Series, 2006, ISBN 1-84628-369-8.
- Lawvere, F. William, "Metric spaces, generalized logic, and closed categories", [Rend. Sem. Mat. Fis. Milano 43 (1973), 135--166 (1974); (Italian summary)
With an author commentary: Enriched categories in the logic of geometry and analysis. Repr. Theory Appl. Categ. No. 1 (2002), 1–37.
- Weisstein, Eric W., "Product Metric" from MathWorld.
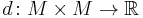
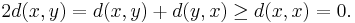
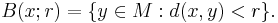
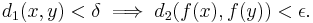
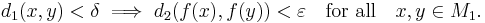
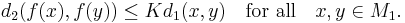
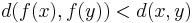
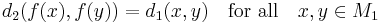
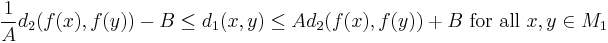
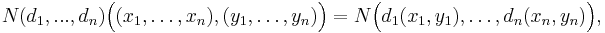
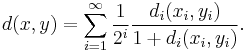
![d'([x],[y]) = \inf\{d(p_1,q_1)%2Bd(p_2,q_2)%2B\dotsb%2Bd(p_{n},q_{n})\}](/2012-wikipedia_en_all_nopic_01_2012/I/6fd9d735172b9c1288bd15d079387655.png)